シェーディング

Ｑ：3次元の分子構造模型を描き，マウスで回転させたりできますか？

Ａ：分子をシェーディングされた球で描く方法は，米澤さん＠京都大 学のサイト gnuplotスクリプトの解説：「上級テクニック （グラフ編）3次元グラフ表面の色付け」に記されていますので，それを応用す れば可能です．ちょっと長いですが，水分子を描くスクリプトを以下に示します．

• スクリプト：H2O_shading.plt

  # 球面の媒介変数関数
  Fx(u,v)=sin(u)*cos(v)
  Fy(u,v)=sin(u)*sin(v)
  Fz(u,v)=cos(u)
  
  # 光の方向
  sx=1.0; sy=1.0; sz=1.0
  
  # 微分用の微小数
  h=0.000001
  
  # Fx,Fy,Fzのuおよびvによる偏微分
  dFxu(u,v)=(Fx(u+h,v)-Fx(u-h,v))/(2.0*h)
  dFyu(u,v)=(Fy(u+h,v)-Fy(u-h,v))/(2.0*h)
  dFzu(u,v)=(Fz(u+h,v)-Fz(u-h,v))/(2.0*h)
  dFxv(u,v)=(Fx(u,v+h)-Fx(u,v-h))/(2.0*h)
  dFyv(u,v)=(Fy(u,v+h)-Fy(u,v-h))/(2.0*h)
  dFzv(u,v)=(Fz(u,v+h)-Fz(u,v-h))/(2.0*h)
  
  # 法線ベクトルの各成分 n = lu x lv
  nx(u,v)=dFyu(u,v)*dFzv(u,v)-dFyv(u,v)*dFzu(u,v)
  ny(u,v)=dFzu(u,v)*dFxv(u,v)-dFzv(u,v)*dFxu(u,v)
  nz(u,v)=dFxu(u,v)*dFyv(u,v)-dFxv(u,v)*dFyu(u,v)
  
  # 光の方向ベクトルsの長さ
  s_length=sqrt(sx**2 + sy**2 + sz**2)
  
  # 法線ベクトルnの長さ
  n_length(u,v)=sqrt(nx(u,v)**2 + ny(u,v)**2 + nz(u,v)**2)
  
  # 光の方向ベクトルsと表面の法線ベクトルnの内積で色を決める：5色
  Hy(u,v) = (n_length(u,v)!=0.0) ? \
    (1.0 + (sx*nx(u,v)+sy*ny(u,v)+sz*nz(u,v))/(s_length*n_length(u,v)))/10.0: Hy(u+h,v+h)
  Ox(u,v) = (n_length(u,v)!=0.0) ? Hy(u,v)+1.0/5 : Hy(u+h,v+h)+1.0/5
  Cb(u,v) = (n_length(u,v)!=0.0) ? Hy(u,v)+2.0/5 : Hy(u+h,v+h)+2.0/5
  Cl(u,v) = (n_length(u,v)!=0.0) ? Hy(u,v)+3.0/5 : Hy(u+h,v+h)+3.0/5
  Me(u,v) = (n_length(u,v)!=0.0) ? Hy(u,v)+4.0/5 : Hy(u+h,v+h)+4.0/5
  Whole(u,v) = u/pi;
  
  # 色使いの指定：5種類
  set palette defined (\
  0.0 "#333333" , 0.2 "#ffffff", 0.2 "#222200", 0.4 "#ff3333",\
  0.4 "#000000", 0.6 "#999999", 0.6 "#003300", 0.8 "#33cc33",\
  0.8 "#002222", 1.0 "#3366cc")
  
  # いったんパラメータファイルを作る
  set xrange [0:pi]
  set yrange [-pi:pi]
  set samples 24
  set isosamples 36
  sphere="sphere.dat"
  set table sphere
  splot 0
  
  # 描画 
  unset table
  set term wxt enh size 400,400
  unset border
  unset tics
  unset colorbox
  unset key
  L = 1.5
  set xrange [-L:L]
  set yrange [-L:L]
  set zrange [-L:L]
  set ticslevel 0
  set orig -0.2,-0.2
  set size 1.4,1.4
  set pm3d depthorder nohidden3d
  set view 70,50
  
  set macro
  Fx="Fx($1,$2)"
  Fy="Fy($1,$2)"
  Fz="Fz($1,$2)"
  Ox="Ox($1,$2)"
  Hy="Hy($1,$2)"
  Cb="Cb($1,$2)"
  Cl="Cl($1,$2)"
  Me="Me($1,$2)"
  
  ### H20
  ay = 0.957*sin(104.5*pi/180/2)
  az = 0.957*cos(104.5*pi/180/2)
  rH = 1.2*0.25   # 酸素と水素がほぼ同じ大きさというは違和感があるので
  rO = 1.4*0.5    # 適当にスケーリングした．根拠は何もなし．
  splot sphere using (0):(0):(0):(Whole($1,0)) with pm3d,\
  sphere using (rO*@Fx):(rO*@Fy):(rO*@Fz+az):(@Ox) with pm3d,\
  sphere using (rH*@Fx):(rH*@Fy-ay):(rH*@Fz):(@Hy) with pm3d,\
  sphere using (rH*@Fx):(rH*@Fy+ay):(rH*@Fz):(@Hy) with pm3d
  
  pause  -1
  

• 表示画面例
  
  
  
  
  
  
  
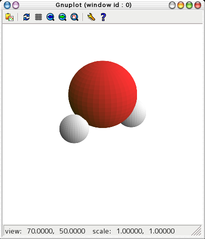
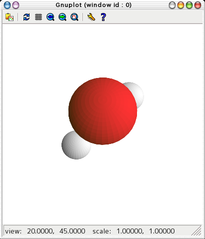
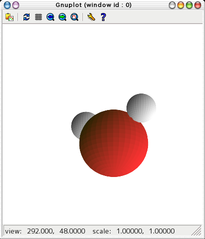
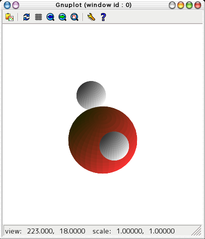
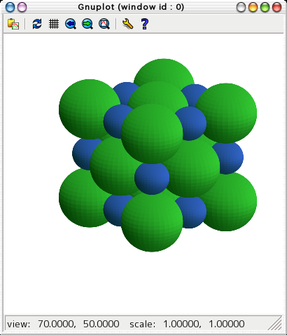
• NaCl型の結晶模型を描画するスクリプト NaCl.pltとその表示結果を示します． 球を27(+1)個描くので，マウスへの反応は非常に鈍いです．
  
  
  
  
  
  
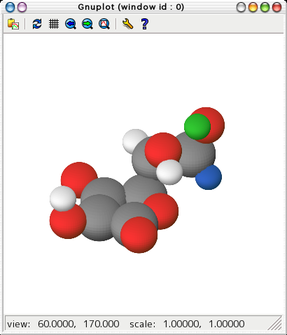
• ビタミンC(Ascorbic酸)の結晶模型を描画するスクリプト VitaminC_phong.pltとその表示結果を示します． 米澤さんのスクリプトにある物理的な反射則に基づかず，それらしく見せる 簡単な色付け関数を採用しています．しかし，結局面素を描く部分が律速である ため，マウス操作性は鈍いままです．なお， 水素（本来白色）の一部の色を変えて，全部で5色描けることをデモしています．
  
  
  
  
  
  
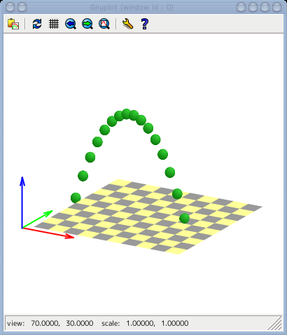
• 放物運動のストロボ撮影風画像を作成するスクリプト paraboric.pltとその表示結果を示します． チェック柄の床の描画に工夫が必要でした．Ver4.4から導入された iterationを使っています．